A reader named Joe asked a question about Japanese text that actually tends to pop up on a regular basis:
Hello. I recently came across a screenshot of animal crossing, and I was confused about something. If you look in the attached picture, it shows regular Japanese text, but for some of the bunches of text, there is text above it in a smaller font. What is up with that?
And here’s the picture Joe attached:
 |
As you can see, there seems to be small text above the regular text there… What the heck is this craziness?!
The quick answer is that the extra text above normal text is basically a pronunciation guide.
There is a little more to it than that, though.
Japanese Writing Systems
In super-simple terms, Japanese writing comes in two forms: kanji and kana.
Kanji originates from Chinese and generally looks a bit complicated, you know, stuff like 影響 and 爆弾 and 馬鹿. There are thousands of kanji characters and each one usually has multiple meanings and pronunciations that you gotta memorize.
Kana is a bit more like a “syllable alphabet” and generally looks simpler, with stuff like この and ハロー and そら. Because it’s based around syllables, kana is usually super-easy to read and pronounce. There aren’t many kana, so you can easily master it in a few days.
Anyway, standard Japanese writing uses a mix of both kanji and kana, as well as a dash of English. The problem is that because Japanese kanji can be read in so many ways, sometimes it’s not always clear which reading is intended. For example, just the basic kanji character 下 has like a dozen possible readings!
 |
So, when a Japanese writer wants to make sure readers know how to pronounce a bunch of kanji, it’s common practice to put the pronunciation in kana above it. This type of kana that appears above kanji is known as furigana.
If we had furigana in English, I suppose it might look something like this:
 |
Anyway, since it takes many years to master all the standard Japanese kanji, it’s normal to see furigana in stuff aimed at kids. That’s why it’s so common in games and manga and such.
But it’s not by any means a kids-only thing. Japanese names are usually written in kanji, and including the pronunciation on your business cards or form applications or whatever else is extremely common. In fact, Japanese names are so crazy that there are huge dictionaries and resources just for name pronunciations!
 |
Basically, have you ever had someone read your name out loud but pronounce it wrong? That problem is much worse in Japanese, so furigana serves as a solution.
Furigana is also super-helpful when it comes to learning the language and when learning kanji. So furigana acts as a crutch sometimes, and as a helpful resource other times. It’s a really neat aspect of the Japanese language!
 |
Furigana Everywhere
Furigana is seriously everywhere in Japanese! It’s in games, of course:
 |  |
…Although due to memory and hardware limitations it’s not very common in older games.
Furigana is also very common in manga and such:
 |  |
Furigana is common in books of various types, too:
 |  |
Furigana is sometimes used on TV:
 |
Furigana is very important when it comes to Japanese karaoke:
 |
Most mainstream newspapers don’t use furigana in the main articles, but it’s still common to see furigana in other parts:
 |
It’s common to see furigana on really important signs too, like train station signs. Many train stations in Japan also helpfully include the names written out in English for folks like us!
 |
So if you ever see small text on top of normal-sized Japanese text, now you know what it is!
Advanced Furigana
By some crazy coincidence, I received another e-mail on the same day by another reader named EmpoleMew that was also about furigana:
To make a long story short, with the extremely minuscule knowledge I have of Japanese, I know that furigana is meant to provide a sort of pronunciation guide to kanji (and foreign characters) that may be unfamiliar or hard to read because of small print. However, as an avid player of Yu-Gi-Oh, I’ve noticed that some Japanese card names have furigana that actually gives the card a name completely different from the kanji. The example that led me to asking the question is a new card, whose name is spoken in the anime and written in furigana on the actual card as “Rank-Up-Magic The Seventh One”, but whose kanji says the name of the card is “Rank-Up-Magic Swords of the Seven Emperors”! Knowing the context of the anime, the Seven Emperors name makes sense, referring to the characters using the card, but this name is never spoken by anyone, and the double name will be lost to localization like many other things in the game.
So the question (or questions I guess) here is, is this a common practice in Japanese media, and can you think of any possible reasons for doing it? Have you ever come across situations like this in any of your translation work, professional or personal? I eventually plan to get into localization work myself in the future, and I feel like this is something I need to be weary of.
So we’ve seen how furigana can tell readers now how to pronounce kanji. But on occasions a writer can use furigana to create a totally custom pronunciation or give extra information – which is actually extremely common in Japanese entertainment!
Just because I happen to have it handy, here’s an example from the Fairy Tail manga:
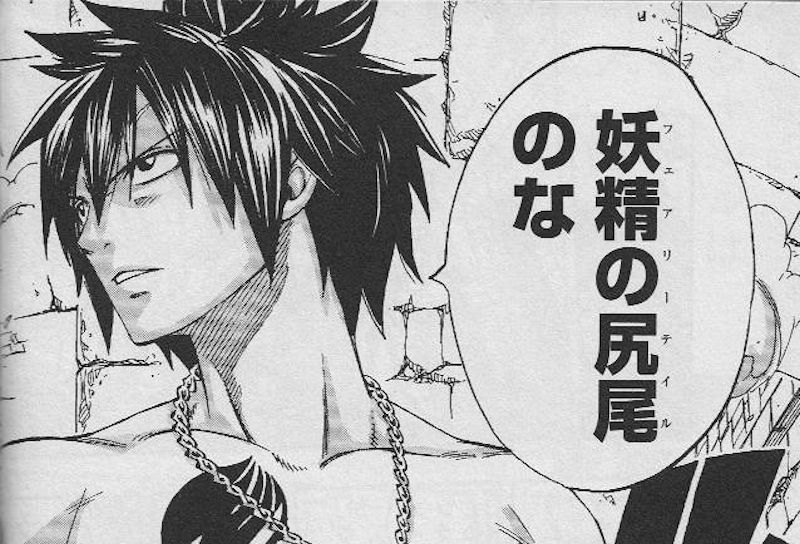 |
Here, he’s saying 妖精の尻尾, which would normally have the furigana of ようせい (yousei, "fairy") and しっぽ (shippo, "tail"). But the author decided to give it a custom pronunciation instead: フェアリーテイル (”fearīteiru”, "”Fairy"). From this, Japanese readers can tell how to pronounce the word and what the word actually means.
Here’s another example:
 |
Here, the highlighted words 滅竜魔導士 and 魔水晶 both have this custom furigana. 滅竜魔導士 is meant to be read out loud as “Dragon Slayer” and 魔水晶 (masuishou) is meant to be read out loud as “lacrima”.
The writer could’ve easily just used “Dragon Slayer” and “lacrima” directly in the text. But with the custom furigana, readers can pronounce it the intended way AND know what these names actually mean. It’s a pretty nifty trick!
So, as a translator, how are you supposed to handle all this double-meaning, double-information stuff? The answer is that it’s pretty much a case-by-case basis, and no matter what you do something will get lost in the translation. I come across it a lot in my own work, so maybe I’ll try to document some cases for a future post. Usually it comes down to personal preference, or, if you’re super-duper lucky, you can ask the company or creator about it.
Anyway, whew! So that’s the quick look at the wacky world of Japanese double-text and the cool stuff it can be used for! Even if you don’t plan on learning Japanese, hopefully this gives you a little more insight on how other languages try to handle the “How the heck do you pronounce this word?!” problem.
To be honest, there’s actually a lot more to furigana than what we’ve seen here; it can often be used for jokes, word play, creating catchy phone numbers, memorable marketing slogans, and more. So who knows, maybe they’ll come up in future articles! But for now let’s let our brains rest a little 😛

![Passport to MOTHER 2 [Learn Japanese!] Passport to MOTHER 2 [Learn Japanese!]](https://legendsoflocalization.com/wp-content/uploads/2018/05/pp-m2.jpg)


A long, long time ago (in a galaxy far away, j/k), back when i used to be into Yu-Gi-Oh, i remember seeing the different pronunciations on cards. I think the one that most comes to mind was the famous Blue-Eyes White Dragon card, which had a kanji name, with some of those furigana things spelling out the english pronunciation above it.
Actually, come to think about it, it really is impressive just how long the Yu-gi-oh franchise has been around. I used to really be into the anime, manga, and card game back when i was in high school, which was eleven years ago. I tried recently to read one of the newer mangas, but i just couldn’t get into it. It really is amazing, though, that other manga authors keep coming up with new stories long after the original manga author put an end to his little tale about an egyption ghost killing people with deadly games.
I was into Yu-Gi-Oh for a month or so, probably about the same time you were (though I was a hair older). I got the original Kaiba starter, and was very fond of my Blue-Eyes White Dragon. It was like one of the few cards I recognised from the small amount of the cartoon I’d seen. 🙂
Potato Girl is being voiced by Ashly Burch, I am excite.
Actually, I’ve been curious about the use of furigana translating into Japanese. Like in Star Wars, apparently (according to this blog: http://nihonshock.com/2009/12/star-wars-quotes-in-japanese/) the Dark Side is called ダークサイド, but written as 暗黒面. Which seems a little silly, as either one alone works fine. Is this like some kinda attempt at localization? Like I know this trend was popular with shonen manga even back then, so I can see some localizers doing this in an attempt to appeal to younger audiences.
I’ve also noticed in some games they forgo writing some words in Japanese and just have the English left untranslated. The only example I can remember off the top of my head is Borderlands 2. If you look on YouTube you can find a video of the game in Japanese with Japanese subtitles, and certain key words like “Bandit” are mixed in with Japanese text.
For the Dark Side thing, I think its to so the audience knows the meaning while avoiding names changes.
I know that, but the point is why not just say 暗黒面? That alone gives the meaning of 暗黒面, quite literally I might add.
Name changes in translation, even when its a group name or title that can be translated otherwise, is a touchy subject in j to e, and I’d imagine it’s the same the other way too. There’s also the possibility that the license to translate the movie prohibited changing names, which isn’t unheard of (very recent example is not being allowed to change Monokuma in Danganronpa).
One of the odder instance of “custom pronunciation” furigana I’ve seen is the back of Summon Night: Craft Sword Monogatari: Hajimari no Ishi (Aka Swordcraft Story 3). The first instance of 物語 is furiganed ストーリ (story) and latter down the box uses 物語 with the normal ものがたり (Monogatari) in furigana.
The manual (excluding some promotional info at the end) also has full furigana, though sadly the game (and the rest of the Summon Night games) lack it.
Oda does that a LOT in One Piece. Like “Grand Line” is “偉大なる航路” and the furigana is “グランドライン”. Luffy’s attacks usually have it also, like it will say “pistol” in kanji and the pronunciation will be as it would be in English in the furigana.
And then on some occasions it gets confusing like with “Gomu Gomu no Redhawk”, it pays tribute in the kanji to Ace by having “火拳” (“fire fist”) in the kanji. Pirate Warriors 2 translated it literally and it’s called “Gum-Gum Fire Fist Pistol” instead of “Gum-Gum Redhawk”.
Hunter x Hunter does it a lot. The alternate furigana text is often something else entirely, and not necessarily katakana for some English equivalent, but text in hiragana. Sometimes those furigana subtitles even includes simple kanji like 一二三四人.. (oh, the irony!)
All manga aimed at younger audiences these days have furigana for all kanji, no exception.
I get it of course, my point was that the furigana in HxH were something completely unrelated in most cases, and sometimes, the furigana (which is supposed to give the reading for complicated kanji in the first place) have kanji themselves.
Right, I misread what you wrote.
Furigana seems to be a near standard on the 3DS, with even “adult” games like Shin Megami Tensei 4 having it (maybe it’s a system font thing?). The exception seems to be Pokemon, which only has a kana only mode or kanji mode with no furigana for some reason.
Custom Robo: Battle Revolution made a leap from the first two game all kana to furigana. (the script seems to be on the english disc still. Wonder if there is an AR code I could force it with, because I’d really like to take a look at how the game was translated as the script is so joke filled while the rest of the series seems to be pretty straight laced)
A related pet peeve of mine is the romanization of long vowels. My stance is to stay true to the original kana spelling, but it seems that doing so is rare in the games I play, and when I see a word romanized by shortening the vowel or using a macron, I have difficulty not noticing it.
For example, while playing Ace Attorney: Dual Destinies for Nintendo 3DS, my stomach turned every time I saw the word “yokai” in the script because I already learned the hiragana spelling: 「ようかい」. That’s “yo U kai”. Knowing how Japanese phonology works, I accidentally misread every instance of “yokai” as 「よかい」 and correct myself every time.
I understand the meaning of the macron and how difficult typing letters with macrons can be, but I believe that romanizations should stay true to the kana spelling, especially in the absence of macrons. A related issue is people misspelling “über” as “uber”, not knowing that they should spell it as “ueber” if umlauts are unavailable or inconvenient.
One more reason for staying true to the kana spelling: I cannot in good faith consider 「えい」 and 「おう」 to be true extended vowels (substitute 「え」 and 「お」 with any kana with the same vowel). I once read in an online guide that, for example, in 「えい」’s pronunciation, the /e/ curves toward /i/, resulting in “ay” instead of “eh”, which makes sense because the kana have different vowel sounds.
However, I have encountered the reverse: In the Famicom RPG “Juvei Quest”, the Japanese version spells the protagonist’s name as 「じゅうべえ」, which clearly looks like “Juubee”, not “Juubei” (ignoring the short U and V in the title). I really do not know what to make of this example. Is the pronunciation of 「ええ」 distinct from 「えい」?
I would appreciate it if an expert would shed some light on my confusion.
One problem is that when it doesn’t look ugly (ueber, doubled vowels in general), it can be quite misleading. “Juubee”, for instance, would be pronounced as “juu-bii”. Even reflexively, by people who know how it should be pronounced. Same thing thing with “oo” (looks like “uu”).
I don’t understand why this has to be an issue. Then again, I minored in Latin and also took Greek, so I don’t have a problem with that range of vowels in odd patterns. I’d rather all the vowels be there and THEN learn if/when/how some are elided. (Then again, maybe my insistence there means I should learn just learn kana)
For someone who wants to learn the language and its writing system, I agree, learning to read “bee” as more like “bay” than “bee” should not be a problem. (Although I still sometimes initially read it as the latter when encountering romaji in the middle of English text, when I’m reading through something that’s been written out in romaji (e.g. a text dump of an all-kana game script), I use the Japanese pronuciation reflexively.)
For localizations, however – where you’re trying to convey the correct pronunciation to someone who is statistically unlikely to have learned or be learning the language, and is nearly as unlikely to care, and may very well not even know that this was in another language to begin with – that sort of rigid, precise, reversible representation of the Japanese will likely not be the optimal solution.
ええ and えい, as well as おお and おう, used to be pronounced differently, but not any more; in both cases, the first’s pronunciation took over.
I got to see a panel about using furigana to convey alternate meanings at Anime Expo ’13–here’s a link to a paper by one of the people on the panel, since it was pretty interesting: http://www.eastasiareview.org/issues/2010/lewis.shtml
Is that some Sexy Commando? Possibly the funniest thing I have ever experienced in my life!
It’s astounding how many visual novels, engines made to handle oodles and oodles of text, don’t have any ruby support at all, let alone for single width characters, and resort to just lazily putting things in parens.
By “ruby” do you mean furigana support? Because I saw that the internal files of many DS games referred to the furigana font as “ruby”.
The always-double-width stuff always baffled me too.
http://en.wikipedia.org/wiki/Ruby_character
Ruby is the internal code tag that I’ve pretty much universally seen for any kind of furigana or furigana-like font.
In Dragon Ball, “Super Saiyan” is written as 超サイヤ人 (Chou Saiyajin), but with furigana スーパー (Suupaa) written over it.
There’s also a villain in Gekkou Kamen called Satan’s Claw, who’s name is written as 魔人の爪 (Majin no Tsume) but with サタン (Satan) written over the 魔人 as furigana.
In some older games like Ocarina of Time, the furigna is put in brackets after the word instead of above it. So it says, for example, コキリの剣(けん) seen here:
http://img1.wikia.nocookie.net/__cb20110624000702/zelda/ja/images/6/68/%E3%82%B3%E3%82%AD%E3%83%AA%E3%81%AE%E5%89%A3.png
I was wondering, is doing it this way standard practice when writing in a place where you can’t put text above text like normal? Like in message boards and whatnot.
I saw it in Tengai Makyou Zero/IV too, and those didn’t have furigana either. The parts where I saw those used were something like:
CHARACTER_NAME (FURIGANA)
(maybe because reading names is too complicated?)
And Tengai Makyou Zero actually had the location names showing when entering a new map actually show the name in kanji, then the text disappears then a new string appears which is the same but written in all hiragana. It’s a nifty solution.
Phantom Hourglass/Spirit Tracks show text in kanji. But each kanji can be tapped on so that a bubble with the furigana appears.
Maybe my memory is playing tricks on me, but I thought Ocarina of Time (or was it the 3DS port/Majora Mask?) did have furigana built in.
Given the rest of the game doesn’t use furigana, it’s more likely so you know 剣 is pronounced “ken” and not “tsurugi”.
And I also wanted to mention Tales of Vesperia, where you have things like “凛々の明星” (Riri no akaboshi) with furigana ブレイブヴェスペリア (Brave Vesperia).
All of the game’s other technical words such as Blastia, Entelexeia, Adophagos, Dein Nomos, etc all have kanji with completely different furigana readings.
Graces f did that too, such as with the terminology words Protos Heis and valkines cryas.
I remember reading about this many, many years ago, on a website all about how the wordplay and jokes in the Harry Potter books were translated across the world. I still can’t quite wrap my head about the “custom pronunciation” aspect of furigana–aparently the Japanese Harry Potter translations use them a LOT–but I suppose it’s more of a cultural thing, and/or a way for the translator to use the original name and a localized one. The first usage of furigana seems pretty handy, though! I was chatting recently with a friend about the cartoon series Gravity Falls, which has a character who is typically referred to as “Soos.” His real name is Jesus, but everyone just calls him “Soos.” We speculated that maybe his real name wasn’t used because of how that would look in promotional material, and how it wouldn’t necessarily be clear that his name was pronounced “Hay-SOOS,” and not like the religious figure. If English had something like furigana, things might’ve been different!
You mean this one?
http://www.cjvlang.com/Hpotter/index.html
Actually, I think it was a different one–the one I looked at covered more languages than Chinese, Japanese, and Vietnamese. Still, I’m not surprised more than one website like this exists! Now I wish I could remember the other site…
I remember that the game Jak 2 for PlayStation has, in the Japanese dub, one section happens to have a subtitle with Precursor writing in one section. It’s a cutscene that takes place in Tomb of Mar if I remember right. What’s curious is that this doesn’t happen in subtitles in other languages, only in Japanese. I wonder what other games and media has unusual writing in subtitles…
In Death Note, the main character is named Yagami Light. His first name is spelled with the kanji for moon, 月, but pronounced like the English word “Light” for no reason (hipster parents, I reckon). He mentions this a few times. I don’t recall if they ever show it with furigana (I haven’t read the manga in Japanese) but it’s the kind of thing like Fairy Tail that would use that technique.
I heard the authors deliberately used crazy names (except Raye Penbar) so that no one would read their name in a murder-based series and get offended.
Still, Backyard Bottomslash is the greatest name ever.
I’ve seen a Harry Potter fanpage about how the books are translated into Asian languages point out in the Japanese version a creative example of furigana being used to convey a pronunciation different from the Kanji that is written. http://www.cjvlang.com/Hpotter/wordplay/knight.html In the third book when Harry is picked up by the Knight Bus, in order to convey the night/knight wordplay in Japanese, the translators call it the 夜の騎士 “yoru no kishi” bus or “Knight of the Night” bus and have furigana above to let readers know that its actual name is supposed to be said like the English word night.
The first couple of episodes of Bobobo-bo Bo-bobo have titles that, while they don’t use furigana, make use of the “custom pronunciations” idea as a source of humor.
I don’t have the first episode handy, but the second is entitled:
「毛涙」と書いて
「センチメンタル」
と読みんでほしい…
The fansub translation of that (which seems reasonable from what I can see) is:
It’s written as “Tears of the Hair”
but I’d like you to read it as
“Sentimental”…
With the understanding that “read” here is in the sense of “pronounce”, as I believe is common terminology when speaking about kanji.
Similar example in a trophy description for Tales of Xillia 2:
「破壊者と書いてブレイカーと読む。」
“It’s written as ‘destroyer’, but read it as ‘breaker’.”
Sometimes, I try to quickly determine a manga’s target audiences by seeing which kanji are furigana’d.
When some people ask what the deal is with reading kanji, I usually just explain it’s like our number system. They just have different rules for it.
Whereas, in English prose, it’s usually bad form for you to write “I went to the store and bought 2 apples”. “2” and “two” are the same, but we as English speakers only use the numbers in text when it’s too big/not intended to be pronounced or if mathematical precision is preferred.
Japanese just happens to have a much larger set of such symbols (which have also accumulated the same ambiguities of non-numeral words), and the rules for using them just happen to be the other way around: that higher-level prose SHOULD use them. They just don’t HAVE to.
I recall it was mentioned in the Detective School Q anime that they have the furigana displayed above kanji for scripts so that actors wouldn’t stumble over pronunciations during rehearsal.
Furrygana, hentaigana… no wonder the Japanese have a reputation of being perverts! I kid, I kid.
So if there’s no furigana, how does one figure out what reading to use? Just based on context?
I guess. In Japanese class, my sensei didn’t really have an answer for the question of which situations 後 should be read as ‘ato’ or as ‘ushiro’. I guess that Japanese people tend not to think about these rules and just go with what sounds most natural.
Actually, there are some guidelines, though it’s a bit complicated.
There are at least two readings (pronounciations) to every kanji (though likely many more). One type is called on’yomi, which is a Japanese approximation of what the original Chinese pronounciation of that character was. The second type is called the kun’yomi, which is a reading that is more in line with the original Japanese meaning of the word.
Ah! There we go, this is a more complete explanation: https://en.wikipedia.org/wiki/Kanji#Readings
For me, the difficulty comes when trying to determine if it’s supposed to be 「あと」 or 「のち」. Seriously, 後 screws me up I think more than any other kanji, haha. It comes up in writing so much but there’s never any furigana so I never get enough examples to be able to get used to which shows up where!
I really hate it, too. The sad part is that some pronounciations are ok in some contexts, but bad in others. Perhaps it’s a bit like avoiding the “shi” and “ku” readings for the number 4 and 9, respectively, because they have connotations of “death” and “suffering” with those readings.
It’s usually just context, yeah. Most words that are made up of multiple kanji are gonna be pronounced the same way each time (not every word, but most words). Single-kanji words can be a little more varying, but each reading usually has its own definition as well, so based on the context you can know what definition it is and therefore which reading to use. Kinda like going through an English sentence and knowing whether to pronounce the word “read” as “reed” or “red”, just on a much larger scale.
Thanks for making an article for my question.
There’s that joke relatively common in gag manga where two people are having a conversation but one word is interpreted differently by each other. I’m guessing that’s done with furigana?
Are you talking about “jokes” where someone interprets a word as something embarrassing as some sort of running gag?
Yeah, when I see stuff like that, I tend to reach the conclusion that Japanese comedy is a “work in progress”. (Their two-man standup acts don’t encourage a change in that opinion.)
I do like the way this question is phrased Mato. Reminds me of the Simpsons episode where the bus driver asks about “Those guitars that are, like, double guitars?”.
Has anyone tried using the bopomofo system when trying to read Chinese. It’s not as widespread as Furigana but still.
One of the wackiest examples I’ve seen was in an episode of Dragon Ball whose title had a ‘?’ question mark used as if it was a kanji. The attached furigana explained the question mark was supposed to be read as ‘fushigi’ (mysterious).
There’s other examples like in Hidamari Sketch x ☆☆☆, where the ☆☆☆ is read ‘hoshimittsu’ (three stars).
I wonder, can you use furigana to turn anything into a word? This is like how when I was learning english, I was pretty fascinated with how you could use any word as a verb and people would understand you.
Dragon Ball got a lot of mileage out of Kanji mispronunciations, especially with Son Goku’s name.
Furigana got used very weirdly in the Japanese subtitled movie of the French movie “Taxi 2”, a comedy. In it is a scene in which French police offers, in preparation for visiting important Japanese people, are taught very badly by their bumbling captain how to say “kon nichi wa”, which he pronounces “kon nichon wa”, which he explains as “con” (French for idiot, and he says another cop’s name as an example), “nichon” (tit/breast, he explains by apologetically referencing a well-endowed woman officer), and “wa” (Bruce Lee-like noise). This is explained through the subtitles by writing the kanji for his explanation (馬鹿 and 乳, if memory serves), which are accompanied by furigana for コン and ニチョン, respectively. I might have some details wrong, this was over 10 years ago, but that was basically how the subtitles by furigana slight-of-hand explained a pun.
This is very common in Sailor Moon as well!
For the second case, I usually think of it as a “role reversal”: instead of telling people what a Kanji word is by giving the kana pronunciation, it tells people what a kana word is by using a Kanji word to explain it.
One example of furigana being used for something other than pronunciation I can think of is in the Metal Gear Solid series, there are terms displayed in the subtitles in kanji (often literal translations) and then the actors will say what the furigana says. In Ocelot’s introduction in Snake Eater, he literally introduces himself as an “ocelot” (山猫) but the furigana and seiyuu read “オセロット”
Messed that up, his unit is referred to this way, he called himself Ocelot in katakana